UIUCTF 2024 Writeups
Team: example.com
Home OSINT Crypto Miscellaneous
Without a Trace Writeup
Description
Information gained from prompt
- server.py file
server.py file contents
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import numpy as np
from Crypto.Util.number import bytes_to_long
from itertools import permutations
from SECRET import FLAG
def inputs():
print("[WAT] Define diag(u1, u2, u3. u4, u5)")
M = [
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
]
for i in range(5):
try:
M[i][i] = int(input(f"[WAT] u{i + 1} = "))
except:
return None
return M
def handler(signum, frame):
raise Exception("[WAT] You're trying too hard, try something simpler")
def check(M):
def sign(sigma):
l = 0
for i in range(5):
for j in range(i + 1, 5):
if sigma[i] > sigma[j]:
l += 1
return (-1)**l
res = 0
for sigma in permutations([0,1,2,3,4]):
curr = 1
for i in range(5):
curr *= M[sigma[i]][i]
res += sign(sigma) * curr
return res
def fun(M):
f = [bytes_to_long(bytes(FLAG[5*i:5*(i+1)], 'utf-8')) for i in range(5)]
F = [
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
]
for i in range(5):
F[i][i] = f[i]
try:
R = np.matmul(F, M)
return np.trace(R)
except:
print("[WAT] You're trying too hard, try something simpler")
return None
def main():
print("[WAT] Welcome")
M = inputs()
if M is None:
print("[WAT] You tried something weird...")
return
elif check(M) == 0:
print("[WAT] It's not going to be that easy...")
return
res = fun(M)
if res == None:
print("[WAT] You tried something weird...")
return
print(f"[WAT] Have fun: {res}")
if __name__ == "__main__":
main()
Running server.py
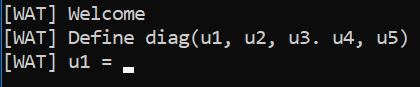
Information Gathering Stage
The first thing we had to do was figure out how the code worked. We realized that the inputs() function would be used to create a matrix where only the diagonal elements would be filled based on user input, and that the handler() and check() functions were used to check the validity of the matrix. Then, We figured out that the fun() function would return the trace (sum of the elements on the diagonal) of the product of the inputted matrix and a matrix where the diagonal elements were filled with pieces of the flag.
Thinking Stage
We figured out that the way to solve this challenge would be to create 5 valid matrices and then use the trace to set up a system of equations and solve for each piece of the flag.
To make this easy, we inputted 11111, 12111, 11211, 11121, and 11112. Outputs, respectively:
1
2
3
4
5
6
7
8
9
10
11
12
13
11111 - 2000128101369
12111 - 2440285994541
11211 - 2426159182680
11121 - 2163980646766
11112 - 2465934208374
b = 2440285994541 - 2000128101369 = 440157893172
c = 2426159182680 - 2000128101369 = 426031081311
d = 2163980646766 - 2000128101369 = 163852545397
e = 2465934208374 - 2000128101369 = 465806107005
a = 2000128101369 - 440157893172 - 426031081311 - 163852545397 - 465806107005
= 504280474484
The Solve
From there, we set up a system of equations using each coefficient we entered and the corresponding traces, solved for the decimal values of the flag, converted those decimals to hex and the hex to ascii, and retrieved the flag.
The flag for Without a Trace is uiuctf{tr4c1ng_&&_mult5!}
Written by @cornguy.
Formatted by @goldenscience